A Neural Network-Based Approach for Approximating Arbitrary Roots of Polynomials
Abstract
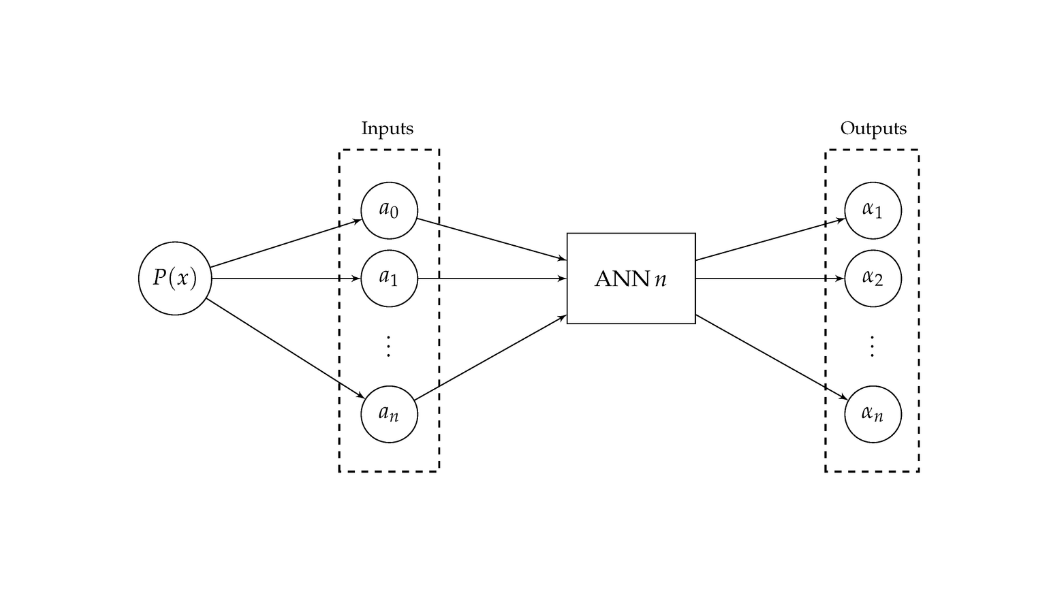
Finding arbitrary roots of polynomials is a fundamental problem in various areas of science and engineering. A myriad of methods was suggested to address this problem, such as the sequential Newton’s method and the Durand–Kerner (D–K) simultaneous iterative method. The sequential iterative methods, on the one hand, need to use a deflation procedure in order to compute approximations to all the roots of a given polynomial, which can produce inaccurate results due to the accumulation of rounding errors. On the other hand, the simultaneous iterative methods require good initial guesses to converge. However, Artificial Neural Networks (ANNs) are widely known by their capacity to find complex mappings between the dependent and independent variables. In view of this, this paper aims to determine, based on comparative results, whether ANNs can be used to compute approximations to the real and complex roots of a given polynomial, as an alternative to simultaneous iterative algorithms like the D–K method. Although the results are very encouraging and demonstrate the viability and potentiality of the suggested approach, the ANNs were not able to surpass the accuracy of the D–K method. The results indicated, however, that the use of the approximations computed by the ANNs as the initial guesses for the D–K method can be beneficial to the accuracy of this method.
More information
- Authors
- Diogo Freitas; Luiz Guerreiro Lopes; Fernando Morgado-Dias
- Date
- 2021
- Journal
- Mathematics
- Special issue
- Intelligent Tools and Applications in Engineering and Mathematics
- Publisher
- MDPI
- Source
- Link
Citation
@article{freitas2021,
author = {Freitas, Diogo and Guerreiro Lopes, Luiz and Morgado-Dias, Fernando},
doi = {10.3390/math9040317},
journal = {Mathematics},
month = {2},
number = {4},
pages = {317},
title = {A Neural network-based approach for approximating arbitrary roots of polynomials},
volume = {9},
year = {2021}
}
